百囚问题

问题描述

#

百囚问题是概率论和组合数学中的一个数学问题。在这个问题中，100 名编号囚犯必须在 100 个抽屉中找到自己的号码才能生存。规则规定，每个囚犯只能打开 50 个抽屉，不能与其他囚犯交流。丹麦计算机科学家 Peter Bro Miltersen 于 2003 年首次提出了这个问题。作为这个问题的升级版本，将有 \(2N\) 名囚犯。他们对应的 \(2N\) 个号码卡被洗牌并放置在 \(2N\) 个抽屉中。每个囚犯最多只能打开一半的抽屉，找到对应自己号码的号码卡。所有囚犯将分别进入房间，任何一个囚犯的失败都会导致整个挑战的失败，囚犯获胜的最大概率是多少?

问题分析

#

随机打开抽屉

#

假设所有囚犯均随机地在 \(100\) 个抽屉里打开 \(50\) 个抽屉。

设随机变量 \(X_i\) 如下。

$$ X_i=\begin{cases} 1\quad \text{There is number i note in 50 drawers.}\cr 0\quad \text{There is no number i note in 50 drawers.} \end{cases} $$

带有自己编号的纸条所在的抽屉满足均匀分布，因此抽到有自己编号的纸条的抽屉的概率 \(P(X_i=1)=\frac{50}{100}=\frac{1}{2}\) 。又由于所有囚犯开抽屉都是独立的，因此所有囚犯均拿到带有自己编号的纸条的概率

$$ \begin{aligned} P(X_1=1,X_2=1,\cdots,X_{100}=1)=&P(X_1=1) \cdots P(X_{100}=1)\cr =&0.5^{100}\cr \approx &7.89 \times 10^{-31} \end{aligned} $$

这个概率显然太低了，甚至低于在 \(1\times 10^{30}\) 个囚犯中选中一个“幸运儿”获得特赦！

按照方法打开抽屉

#

引理1：将抽屉的编号视为数值，将纸条的编号视为指针，则房间内存在且仅存在若干的环。

引理2：若无次数限制，每个人都能以该方法找到带有自己编号的纸条，即有自己编号的纸条一定在自己走的环中。

此时我们可以将问题转化为，假设囚犯均根据上述方法行动，求所有囚犯获得特赦的概率 \(P\) 。由引理2，我们可以进一步将问题抽象为：在 \(100\) 个随机编号 \(1-100\) 的结点所形成的若干个环中，求所有环的长度不超过 \(50\) 的环概率 \(P\) 。

一般情况

#

通过对百囚问题的理论分析，我们进一步分析了这一问题的一般解决方案，即 \(2N\) 囚犯的最佳策略。

当有 \(2N\) 名囚犯，通过 按照方法打开抽屉 分析，我们可以给出以下最优策略。\(2N\) 名囚犯随机标记 \(2N\) 个抽屉。当每个囚犯进入房间时，他们选择与自己标签相同数字的抽屉，取出便条，并继续打开与便条上数字相同的抽屉，如此循环。

如果抽屉 \(k\) 中的数字是 \(s\)，那么这种策略可以表示为 \(f(s)=k\)，其中 \(f\) 是一个从抽屉编号到数字编号的映射，即从当前抽屉到下一个抽屉。这个映射具有以下特性:

$$ \exists i, 1 \leq i \leq 2N, \underbrace{f \circ \cdots \circ f}_{i \text{ times}}(s) = s $$

目前，囚犯成功的条件是:

$$ \forall s, 1 \leq s \leq 2N, \exists i, 1 \leq i \leq N, \underbrace{f \circ \cdots \circ f}_{i \text{ times}}(s) = s $$

对于任何数字，通过应用该函数 \(i\) 次，它都可以映射到自身。

因此，这种策略的样本空间是所有可能的映射集合。有 \(2N!\) 种可能的排列。如果至少需要 \(m\) 次映射，某个数字才能映射回自身，那么我们有以下情况的数量。

$$ C_{2N}^m \cdot (m-1)! \cdot (2N-m)! = \frac{(2N)!}{m} $$

The probability that a number can return to itself after at least m mapping is

$$ P(m) = \frac{\frac{(2N)!}{m}}{(2N)!} = \frac{1}{m} $$

当 \(m \ge N+1\) 时，各种情况是互斥的，因此囚徒成功的概率如下：

$$ P = 1 - \sum_{m=N+1}^{2N} \frac{1}{m} $$

应用与实验

#

百囚问题验证

#

根据 按照方法打开抽屉 中的理论分析，我们可以进一步推断。如果存在长度大于 \(50\) 的环，那么这样的环的数量必须是 \(1\) ，因此我们考虑长度大于 \(50\) 的环的存在概率 \(P’\) 。显然，这两个事件是互补的，所以 \(P = 1 - P’\) 。

首先，考虑一个长度为 \(100\) 的循环。如果循环在任何一点被打断，则有 \(A_{100}^{100}=100!\) 种方式。然后，如果循环被重新连接，循环上的任何一点都可以被视为起点，即循环旋转被视为同一种情况，所以实际的情况数为 \(\frac{100!}{100}\) 。在 \(100\) 个抽屉中随机放置 \(100\) 个纸条的总情况数为 \(A_{100}^{100}={100!}\) 。因此，长度为 \(100\) 的循环出现的概率为：

$$ P_{100}=\frac{\frac{100!}{100}}{100} = \frac{1}{100} $$

同样地，考虑一个长度为 \(k (k > 50)\) 的循环周期。首先，选择 \(k\) 个元素作为循环周期的元素，共有 \(C_{100}^k\) 种方式；将它们在循环周期上随机排列，共有 \(\frac{k!}{k}\) 种方式；剩余的 \(100-k\) 个元素随机分配，共有 \((100-k)!\) 种情况；因此，具有长度为 \(k\) 的循环周期的情况数为：

$$ C_{100}^k \cdot \frac{k!}{k} \cdot (100-k)! = \frac{100!}{k} $$

因此，长度为 \(k\) 的循环的概率是：

$$ P_k=\frac{\frac{100!}{k}}{100!}=\frac{1}{k} $$

由于长度为 \(k (k > 50)\) 的循环的存在情况彼此独立，\(P’=\sum_{i=51}^{100} P_i\)，并通过计算机程序可以得到 \(P’ \approx 0.688\)。

以下是 C 语言代码:

#include <stdio.h>
int main() {
    double sum = 0;
    for (int i = 51; i <= 100; i++) {
            sum = sum + 1.0 / i;
    }
    printf("sum=%lf\n", sum);
    return 0;
}

结果如下：

gcc sum_p.c - o sum_p &&./ sum_p
sum = 0.0688172

因此，\(P=1-P’\approx 0.312\)，这种方法显然比 随机打开抽屉 的概率为\(7.89 \times 10^{-31}\)更可行。

验证一般情况

#

使用 MATLAB 仿真验证计算结果。当囚犯人数为 \(2-50\) 时，对于每种情况，模拟 \(10000\) 次并统计释放囚犯的频率，以获得图中的曲线。

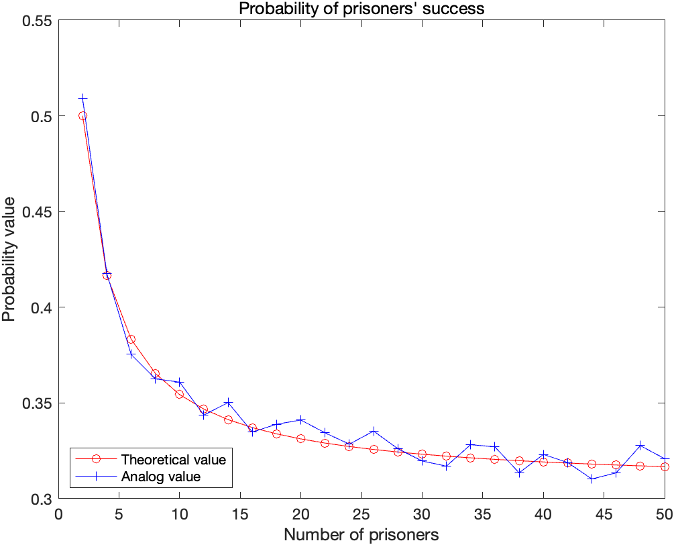
红色曲线根据 一般情况 中的 \(P=1-\sum_{m=N+1}^{2N} \frac{1}{m}\) 绘制，蓝色曲线通过模拟得到。模拟得到的结果与理论计算值大致相同，验证了理论计算的正确性。

以下是 MATLAB 代码：

loop_times = 10000;
theo_prob = [];
simu_prob = [];

for i = 2:2:50
    total = 0;

    for k = i / 2 + 1:1:i
        total = total + 1 / k;
    end

    theo_prob = [theo_prob, 1 - total];
    not_release = 0;

    for j = 1:1:loop_times
        draw = rand([i, 1]);
        [temp, draw] = sort(draw);
        flag = 0;

        for n = 1:1:i
            index = n;

            for m = 1:1:i
                index = draw(index);

                if (index == n) && (m <= i / 2)
                    break
                elseif (index == n) && (m >= i / 2 + 1)
                    flag = 1;
                    n = i + 1;
                    break
                end

            end

        end

        not_release = not_release + flag;
    end

    simu_prob = [simu_prob, 1 - not_release / loop_times];
    i;
end

x = 2:2:50;
plot(x, theo_prob, 'ro-')
hold on;
plot(x, simu_prob, 'b+-')
legend({'Theoretical value', 'Analog value'}, 'Location', 'southwest')
title("Probability of prisoners' success")
xlabel("Number of prisoners")
ylabel("Probability value")

缩放公式 \(P=1-\sum_{m=N+1}^{2N}\frac{1}{m}\) 会得到以下结果。

$$ P > 1-\int_{N+1}^{2N} \frac{1}{dx} = 1-\ln 2 \approx 0.307 $$

这意味着这个概率的下限为\(1-\ln2\)。

结论

#

根据上述计算结果，我们知道即使囚犯数量更多，所有囚犯仍然有近三分之一的成功概率 —— 这与我们最初的直觉相悖，起初我们的直觉告诉我们，让100个囚犯找到自己的编号几乎是不可能的。这种策略的关键在于将所有人的结果集合在一起，尽可能共同成功或失败。最终只有两种可能：存在长度大于50的循环，或不存在。因此只有两种结果：完全胜利或完全失败 —— 没有只有少数人失败的结果。